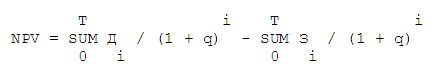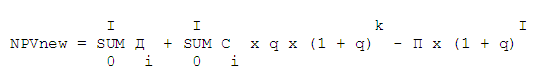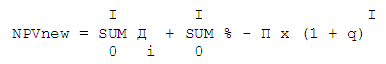Расчет NPV: скрытые недостатки формулы
Концепция стоимости денег во времени основывается на следующем главном принципе: некоторое количество денежных средств стоят дороже сейчас, чем то же количество денег в будущем, так как деньги сегодня могут быть инвестированы, и это принесет дополнительную прибыль. На этом принципе основан подход к оценке экономической эффективности инвестиционных проектов, кроме того, он является одним из основных положений теории финансов и инвестиционном анализе.
Также, считается, что стоимость денег со временем изменяется с учетом нормы прибыльности на финансовом рынке. В качестве нормы прибыльности, как правило, выступает норма ссудного процента.
Учитывая то что, инвестиционная деятельность растянута во времени, в инвестиционной практике принято сравнивать стоимость денег на начальном этапе со стоимостью денежных средств при их обратном получении в виде прибыли получаемой в будущем. В инвестиционном анализе для определения данных показателей используются два базовых понятия: «настоящая стоимость денег» и «будущая стоимость денег».
Будущая стоимость денег это сумма денежных средств, в которую превратятся инвестиции, вложенные сегодня, через какой-то промежуток времени с учетом определенной процентной ставки. Расчет будущей стоимости денег связан с наращением (compounding) начальной стоимости, иными словами это постепенный рост инвестированной суммы за счет присоединения к первоначальной сумме процентных платежей (капитализация процентов).
В инвестиционных расчетах процентная ставка платежей применяется не только как инструмент наращения стоимости денежных средств, но и как измеритель степени доходности инвестиционных операций.
Настоящая стоимость денег – сумма будущих денежных поступлений, приведенных к текущему моменту времени с учетом определенной процентной ставки, т. е. дисконтирование денежных потоков.
И самое главное, основным показателем, показывающим абсолютную эффективность вложений, в тот или иной проект является чистая приведенная стоимость или чистая текущая стоимость (NPV).
NPV использует концепцию стоимости денег во времени и если вложения связанные с предстоящей реализацией проекта, осуществляют в несколько этапов (интервалов), то расчет показателя NPV представляет собой разницу между приведенной стоимостью доходов и расходов. Формула расчета NPV имеет вид:
где,
NPV - чистая приведенная стоимость;
Дi - доход за i-й период времени;
Зi - расход за i-й период времени;
q - коэффициент дисконтирования;
T - время жизни проекта.
Рассмотрим пример. Пусть у нас имеется проект по строительству завода, который будет производить нейтрализаторы выхлопных газов для автомобилей, работающих на бензине. После детального прогнозирования всех будущих затрат и доходов мы получили таблицу, где и произведем расчет чистой приведенной стоимости инвестиционного проекта при ставке налогообложения, равной 35%, и коэффициенте дисконтирования – 2%.
Таблица 1. Расчет NPV проекта (млн. руб.)| Квартал | Капитальные вложения | Затраты на сырье и материалы | Издержки производства | Расходы на зарплату | Доход от продаж продукции | Налоги и прочие отчисления | Результат | Приведенный результат |
|---|---|---|---|---|---|---|---|---|
| 1 | -50,0 | -50,0 | -49,0 | |||||
| 2 | -100,0 | -100,0 | -96,1 | |||||
| 3 | -150,0 | -150,0 | -141,4 | |||||
| 4 | -50,0 | -50,0 | -46,2 | |||||
| 5 | -12,0 | -4,0 | -8,0 | 120,0 | -33,6 | 62,4 | 56,5 | |
| 6 | -12,0 | -4,0 | -8,0 | 120,0 | -33,6 | 62,4 | 55,4 | |
| 7 | -12,0 | -4,0 | -8,0 | 120,0 | -33,6 | 62,4 | 54,3 | |
| 8 | -12,0 | -4,0 | -8,0 | 120,0 | -33,6 | 62,4 | 53,3 | |
| 9 | -15,0 | -4,0 | -10,0 | 150,0 | -42,4 | 78,7 | 65,8 | |
| 10 | -15,0 | -4,0 | -10,0 | 150,0 | -42,4 | 78,7 | 64,5 | |
| 11 | -15,0 | -4,0 | -10,0 | 150,0 | -42,4 | 78,7 | 63,3 | |
| 12 | -15,0 | -4,0 | -10,0 | 150,0 | -42,4 | 78,7 | 62,0 |
Чистая приведенная стоимость (NPV) проекта будет равна 142,43 млн. рублей Нетрудно показать, что увеличение ставки дисконтирования уменьшает величину чистой приведенной стоимости и наоборот. Уменьшение ставки налогообложения приводит к увеличению NPV.
Экономический смысл чистой приведенной стоимости заключается в следующем. Если NPV проекта больше нуля, то проект дает положительный результат по отношению к настоящему времени. Если же NPV меньше или равна нулю, то за реализацию этого варианта не стоит и браться: время сведет на нет все наши усилия. NPV широко применяется во всем мире и входит в систему международных стандартов.
Не стоит, однако, преувеличивать роль и значение этого показателя: ведь при его использовании мы оперируем мнимыми или подразумевающимися величинами. В реальной жизни 100 тыс. рублей, заработанные нами через 2 года, будут иметь свою собственную абсолютную ценность. Увидев эту сумму на нашем счете в банке, мы вряд ли задумаемся, насколько весомой она нам казалась в далеком прошлом.
А теперь попытаемся глубже вдуматься в суть этого показателя. Вышеприведенная формула NPV – это разность двух выражений:
– это дисконтированная сумма доходов.
– это выражение если задуматься не имеет экономического смысла: мы можем дисконтировать доходы, но дисконтирование затрат – это абсурд!
Вплоть до настоящего времени на это обстоятельство никто не обращал внимания, совершенно не задумываясь над смыслом производимых вычислений. Да, действительно, затраты будущих периодов дают нам некоторую экономию по сравнению с затратами настоящего момента. Но как ее правильно посчитать?
Рассмотрим еще один пример. Предположим, что мы финансируем проект из собственных средств. Суммарные затраты равны одному миллиону рублей. Кроме того, в соответствии с планом капитального строительства эти расходы распределены между четырьмя временными периодами: 200 000 руб.; 300 000 руб.; 300 000 руб.; 200 000 руб.
Ставка дисконтирования равна 5 процентным пунктам. Необходимо определить тот эффект, который дает такое распределение затрат во времени:200 000/(1+0,05)1+300 000/(1+0,05)2+300 000/(1+0,05)3+200 000/(1+0,05)4=886277 рублей.
Экономия, таким образом, составит 1000000 - 886277 = 113 723 рублей. А теперь попытаемся подсчитать эффект по новой методике, которая будет иметь вполне определенный экономический смысл.
Предположим, что перед началом капитального строительства 1000000 находились на банковском счете и в конце каждого периода времени на остаток средств начислялся процент, равный ставке дисконтирования. В этом случае получается что, последние 200 тыс. рублей принесут доход за 4 периода равный:200 000/(1+0,05)4 - 200 000 = 43101 рубль.
Аналогично просчитаем эффект для остальных сумм:
- 300 000/(1+0,05)3 - 300 000 = 47288 рублей;
- 300 000/(1+0,05)2 - 300 000 = 30750 рублей;
- 200 000/(1+0,05)1 - 200 000 = 10000 рублей.
Суммарный эффект будет равен 131 139 рублям (сравните с 113 723 руб. по традиционной методике).
Что позволяет нам говорить о применении модифицированной формулы определения чистой приведенной стоимости NPV:

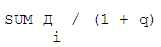 -
сумма дисконтированных доходов;
-
сумма дисконтированных доходов;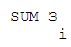 -
сумма реальных затрат;
-
сумма реальных затрат;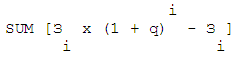 -
сумма реальной экономии от разнесения потока затрат во времени.
-
сумма реальной экономии от разнесения потока затрат во времени.
Нетрудно показать, что при прочих равных условиях модифицированная формула NPV > NPV. Таким образом, мы пришли к очень важному выводу: традиционный показатель NPV, во-первых, не имеет экономического смысла, а во-вторых, будучи применен на практике, дает заниженную оценку. То есть за многие десятилетия его использования западными и отечественными экономистами было отброшено огромное количество перспективных проектов из-за того, что их чистая приведенная стоимость была якобы низка.
А теперь продолжим наши рассуждения. Оказывается, что даже модифицированная формула имеет существенные изъяны. Совершенно непонятно, например, что же впоследствии происходит с процентами, полученными за счет разнесения во времени потока затрат? Кроме того, с точки зрения формальной логики наш показатель NPV противоречив: сумма дисконтированных доходов – величина условная, приведенная, а сумма затрат и сумма экономии от разнесения потока затрат во времени – величины реальные. Сравнивать условные и реальные цифры не совсем некорректно. Необходимо так изменить модифицированную формулу NPV, чтобы она, во-первых, была логически непротиворечива, а во-вторых, полнее отражала реальное положение вещей.
Предположим, что, как и в предыдущем примере, у нас имеется один миллион рублей на банковском счете. Это – совокупная величина наших затрат, которые разнесены на четыре временных периода. После этого наш проект в течение шести периодов приносит прибыль. Для каждого временного периода подсчитаем сальдо счета. Предположим далее, что банк начисляет нам на это сальдо процент, а полученную сумму процента мы в свою очередь также кладем на депозит. Наша совокупная прибыль складывается, таким образом, из доходов проекта плюс доходы от процентов. Однако необходимо сравнить эту прибыль с исходной суммой, также положенной на депозит под сложный процент. Это сравнение методологически корректно, так как мы просто-напросто сопоставляем результат от двух предполагаемых вариантов вложения исходной суммы: первый вариант – «с проектом» (деньги инвестированы в производство), второй – «без проекта» (деньги на депозите). Таким образом, наш новый показатель уже включает в себя как составную часть сравнение по методу «с проектом – без проекта».
где,
I - время жизни проекта (количество временных периодов);
SUM Дi - сумма реальных доходов;
- сумма дохода от процентов на остаток по счету;
k - коэффициент, равный I - i.- доход от первоначальной суммы, положенной на депозит под сложный процент;
Рассмотрим пример расчета NPVnew проекта. Пусть у нас есть начальная сумма в 1 000 000 руб. Инвестиционный цикл содержит в себе 10 временных периодов, q = 5%.
Таблица 5. Подсчет NPVnew проекта (руб.)
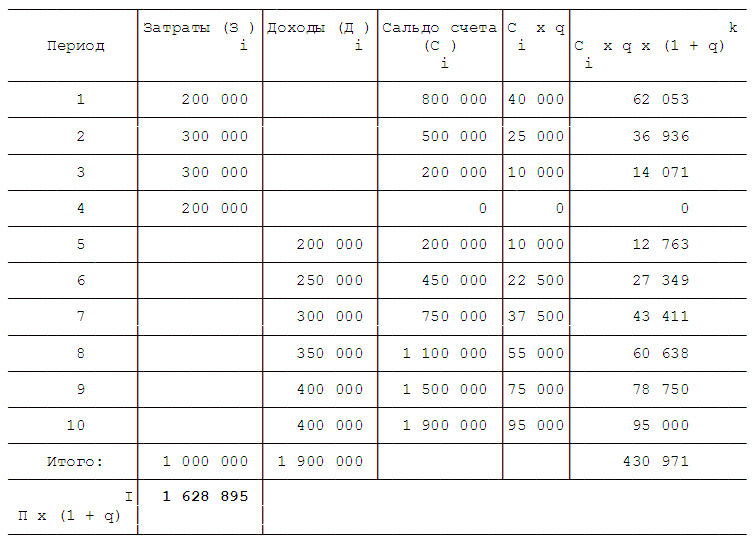
В результате произведенных вычислений имеем NPVnew = 702007 рублей, доходность проекта (Д) = 13,31% за период времени i. Если мы не можем получать проценты по остатку на счете, то из вышеприведенной формулы надо исключить сумму дохода от процентов на остаток по счету.
Экономический смысл NPVnew состоит в следующем. Если этот показатель больше нуля, значит, проект имеет смысл реализовывать, так как это принесет больший доход, чем положенные на банковский депозит исходные средства. Если же NPVnew меньше нуля, то суетиться не стоит – выгоднее просто разместить денежные средства в банке.
Данный показатель легко модифицировать. Если предположить, что мы помещаем первоначальную сумму на депозит на периодов времени с доходностью q за один период, то доход от первоначальной суммы, положенной на депозит под сложный процент примет форму: П + q * I.
Если предположить, что мы не можем получать проценты на проценты с остатка на счете, то сумма дохода от процентов на остаток по счету упростится: SUM Сi * q. Если предположить, что банк не начисляет проценты на остаток по счету, тогда сумму доходов от процентов на остаток по счету следует исключить из формулы. Таким образом, можно записать упрощенный вариант NPVnew:
где,
I - время жизни проекта (количество временных периодов);
SUM Дi - сумма реальных доходов;
SUM % - сумма дохода от процентов на остаток по счету;
- доход от первоначальной суммы, положенной на депозит под сложный процент.
NPVnew оперирует только реальными величинами – доходами, расходами и банковскими процентами, не прибегая к дисконтированию. Таким образом, мы избавляемся от условных цифр.
Автор: К.С. Царихин, к. э. н., доцент Академии
труда и социальных отношений
Источник: Методический журнал «Инвестиционный банкинг» № 2/2009