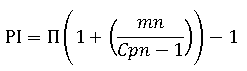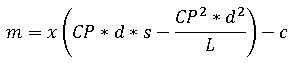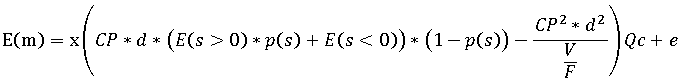Факторная модель анализа эффективности инвестиций

Российской практикой деятельности на финансовых рынках не выработано четкой методологии оценки действий инвестиционного менеджера, т.к. отечественный финансовый рынок еще недостаточно зрел, чтобы современные технологические решения в области доверительного управления заметно влияли на мнение клиентов относительно перспектив вложений в него. Это является основной причиной, по которой инвестиционные компании не стремятся освоить новейшие достижения западных управляющих компаний и создавать собственные, которые вырабатывают значительное количество высокоэффективных методик анализа деятельности сотрудников и сторонних портфельных управляющих. Из разработок зарубежных финансистов в этой сфере отдельно стоит отметить модель анализа производительности управляющих фондами BARRA.

Общий подход к оценке эффективности управления инвестициями

Первоначально стоит классифицировать виды оценок действий инвестиционного менеджера по отношению оценщиков к объекту оценки:

1. Внешняя оценка – предполагает использование минимального набора общедоступных (публичных) данных о деятельности менеджера.

2. Внутренняя оценка – предполагает использование конфиденциальных данных о деятельности менеджера, в т.ч. составляющих элементов его инвестиционной стратегии.

Общий подход к внешней оценке эффективности действий инвестиционного менеджера подразумевает количественную оценку доходности управления инвестиционным портфелем. При данном подходе конечным итогом оценки станет информация об уровне общего дохода за анализируемый период, об уровне избыточной доходности (под которой подразумевается разница между доходностью операций по портфелю и безрисковой ставкой доходности или среднерыночной доходностью данного класса активов), принесенной менеджером, и о величине некоторых коэффициентов доходность/риск, измеренных и экстраполированных с помощью элементов классических эконометрических методов:

1. Простая модель линейного тренда.
2. Простая экспоненциальная модель.
3. Линейная авторегрессионная модель[11].

Полученные данные сравниваются с некими эталонными показателями, в частности:

• Доходностями эталонных портфелей.
• Рыночными индексами.
• Индексами инвестиционных стилей.
• Показателями отношения доходности к риску, которые  одновременно являются однофакторными моделями оценки производительности инвестиционной стратегии.

На практике внешние пользователи инвестиционной информации также зачастую оперируют простейшими однофакторными моделями оценки избыточной доходности, основанными на модели САРМ и методах математической статистики, наиболее известными из которых являются:

1. Индекс Трейнора, рассчитываемый по формуле:

Itr = (PI-RF) / Pβ

2. Индекс Шарпа, рассчитываемый по формуле:

Ish = (PI-RF) / σ

3. Индекс Дженсена, рассчитываемый по формуле:

E(PI)-RF = PIα + Pβ x (E(PM)-RF) + e

Где,
PI - доходность портфеля;
RF - безрисковая ставка;
Pβ - бета-коэффициент портфеля;
σ - стандартное отклонение доходности портфеля;
E(PI) - ожидаемая доходность портфеля;
PIα - доходность в результате действий менеджера;
E(PM) - ожидаемая среднерыночная доходность;
e - случайные флуктуации доходности.

На основании сравнения с эталонными показателями делается вывод об эффективности действий инвестиционного менеджера постфактум. Основным недостатком данного подхода является использование малоинформативных данных, вследствие чего возможны неверные или тривиальные выводы относительно результатов управления [5]. Кроме того, в процессе анализа невозможно выделить факторы, влияющие на результат инвестирования, и ответить на следующие принципиально важные вопросы:

С учетом риска, связанного с активными действиями по управлению инвестициями, какова эффективность работы менеджера?

Каким образом менеджеру удалось достигнуть указанного в отчете уровня доходности? Иначе, каковы источники избыточной доходности?

Каков потенциал инвестиционной стратегии при существенном изменении объема капиталовложений в нее?

Ответить на подобные вопросы можно, лишь получив доступ к данным о составляющих элементах инвестиционной стратегии при проведении внутреннего анализа эффективности и построив многофакторную модель образования доходности. Отметим, что по результатам такого анализа внешним пользователям инвестиционной информации может быть представлен подробный отчет без угрозы для управляющей компании в виде возможной утечки информации о применяемых методах.

Общий взгляд на модели факторного анализа эффективности управления инвестициями BARRA

Избыточная доходность управления инвестиционным портфелем возникает тогда, когда менеджер принимает некоторые активные действия, составляющие его стратегию. В соответствии с подходом, предложенным Ф. Фабоцци для описания действий инвестиционных менеджеров, различают три группы источников избыточной доходности инвестиционных операций:

1. Отслеживание краткосрочных факторных трендов.
2. Отслеживание ситуации на рынке.
3. Фундаментальный анализ финансового инструмента.

Изначально мы будем предполагать, что не существует эталона для сравнения, и выбор будет осуществляться между набором инвестиционных стратегий, с целью распределить имеющиеся финресурсы между ними наиболее эффективно.

Для уточнения источников возникновения избыточного дохода детализируем совокупность факторов, влияющих на цену финансового инструмента. Для упрощения анализа в дальнейшем мы будем использовать только краткосрочные, влияющие на структуру ценового графика факторы, игнорируя фундаментальные тенденции и различия, присущие разнообразным классам активов. Иными словами, мы будем работать с абстрактным классом активов, доходность которого определяется только краткосрочными факторными трендами и флуктуациями, которым подвергаются характеризующие их значения, дабы избежать «подгонки» модели под анализ инвестиций в конкретный инструмент и игнорирования особенностей остальных.

В качестве отправной точки построения факторной модели рассмотрим модель компании BARRA E2 (BARRA Performance Analysis Factor Model) прогнозирования курса акций, разработанную в начале 1970-х гг. Барром Розенбергом и Винейем Маратом.

Каждый индекс формируется исходя из фундаментальных данных, описывающих различные аспекты измеряемого по модели BARRA риска. Их комбинирование приводит к многофакторной мере риска, которая наиболее точно характеризует измеряемое понятие. Индивидуальные данные называются дескрипторами. На основе их комбинирования и составляются 13 рисковых индексов (показателей) на основе 70 простейших: изменчивость рынка, успех компании, размер компании, торговая активность, потенциал роста, отношение дохода к цене акций, отношение балансовой стоимости к цене акций, финансовый рычаг, интенсивность труда, доходность бизнеса и капитализация. Затем методом построения уравнения регрессии были получены коэффициенты влияния для каждого из факторов-переменных. При графической иллюстрации модель имеет вид дерева, на вершине которого курсовая стоимость акции.

В дальнейшем в ряд продуктов компании были включены многие другие модели, а сама модель была неоднократно модифицирована.

Для каждого из параметров модели рассчитывается доверительный уровень вероятности. Формализованная модель имеет вид [1]:

r = xm • rm + xi • ri + xs • rs + xa • ra + er

Где,
r - доходность, полученная за счет фактора;
x - влияние фактора на акцию;
er - необъясненная доходность.

Данная модель применяется институциональными инвесторами, действующими в большей степени пассивно, т.е. вклад инвестиционного менеджера проявляется лишь в самом начале инвестиционного цикла. Кроме того, высокий уровень доходности стратегий на рынке акций обусловлен общим ростом стоимости класса активов, а не действиями инвестиционного менеджера[12]. Для наших же целей мы сделаем попытку формализовать модель, в которой будет отсутствовать такой «влиятельный» помощник, как рыночная доходность класса активов, ввиду того, что действовать мы будем на абстрактном финансовом рынке с нулевой безрисковой ставкой доходности. Кроме того, мы более детально рассмотрим влияние вероятностных факторов на доходность инвестиционной стратегии.

Определение композитных факторов, влияющих на доходность инвестиционной стратегии

Если в случае с рыночной моделью образования доходности и ее производными мы полагаем, что доходность является результатом действия по большому счету только одного фактора – рыночной доходности, то применительно к большинству современных инвестиционных алгоритмов это утверждение окажется ложным, т.к. в настоящее время большое распространение получили рыночно-нейтральные стратегии и так называемые HFT-стратегии. Именно поэтому включение в модель рыночной доходности не всегда корректно.

Рыночно-нейтральная стратегия – стратегия, доходность которой не зависит от среднерыночной доходности данного класса активов.

HFT-стратегии – High Frequency Trading стратегии – операции, совершаемые с частотой, превышающей 1 операцию в минуту во время действия.

Чтобы избежать субъективизма в выделении факторов, рассмотрим такую модель, в которую входили бы априорно оказывающие влияние на результат факторы. Итак, детерминируем доходность как прирост стоимости инвестированного капитала в результате совершения определенного количества операций в течение инвестиционного цикла T. Иными словами:

PI = (CPt-CP0) / CP0

Где, CP - стоимость капитала в период t, t принадлежит T

Далее сделаем первое приближение построения факторной модели через определение рисков, связанных с осуществлением инвестиционных операций. Очевидно, что доходность за инвестиционный цикл является суммой доходностей всех операций за этот цикл, тогда как доходность может принимать как положительное, так и отрицательное значение. Вышеприведенная формула (PI) эквивалентна формуле:

PI = ((CP0-SUMmn) / CP0) - 1

или

PI =SUMmn / CP0

Где, m - абсолютный прирост дохода в серии сделок n, n принадлежит N.

Эта формула корректна в случае, если в течение инвестиционного периода t не производилось реинвестирование дохода. В противном случае доходность нарастает экспоненциально и описывается формулой:

Однако, не ясно, под воздействием каких факторов формируется величина m абсолютного прироста доходности? Также очевидно, что доходность инвестиционной операции логично представить как разницу между ценой совершения операции и ценой прекращения операции, т.е. как эффективно пройденное ценой расстояние в пунктах, умноженное на доходность на один пункт. Графически эффективное расстояние, т.е. фактическую разницу между ценой осуществления (открытия сделки) и ценой прекращения (закрытия сделки) операции, можно представить следующим образом.

Рассмотрим следующую формулу[10]:

m = h x (s - z) - c

Где h - доход на ценовой пункт финансового инструмента; s - ценовой сдвиг; z - величина проскальзывания; c - трансакционные издержки.

Формула не дает ответа на вопрос, чем определяются переменные дохода на ценовой пункт и проскальзывание. Доходность на ценовой пункт определяется как объем сделки, умноженный на x (минимально возможное ценовое движение). Стоит заострить внимание на таком явлении, как проскальзывание.

Проскальзывание возникает вследствие невозможности рынка ввиду недостаточной моментальной ликвидности (ликвидность рынка в расчете на один ценовой пункт) поглотить размещаемый на рынке в результате совершения инвестиционной операции капитал. Для совершения сделки необходимо наличие контрагента, а на рынке в данный момент отсутствует необходимое количество встречных заявок на покупку или продажу, сделка может быть исполнена только тогда, когда совокупный объем встречных заявок становится равен объему открываемой сделки. Задержка обусловливается тем, что торговые заявки поступают на рынок неравномерно, в зависимости от движений цены в различные моменты времени, т.е. на каждый пункт движения цены приходится определенное количество выставленных заявок. Расчет параметров моментальной ликвидности выходит за рамки данной работы, однако для целей построения факторной модели доходности сделки может применяться переменная моментальной ликвидности. Заменяя переменные h и z и раскрывая скобки, опишем доходность формулой:

Где, d - доля капитала, участвующая в серии сделок; L - моментальная ликвидность.

Задавая объем размещаемого в сделке капитала как произведение стоимости капитала на его долю, можно получить возможность оценивать влияние прироста стоимости на доходность инвестиционной стратегии. Из вышеприведенной формулы видно, что величина дохода в сделке графически иллюстрируется отрицательной параболой. Решая уравнение с нулевым m и постоянными s и L, мы можем найти объемы капитала, при которых доход в сделке будет равняться нулю, а также вершину параболы, в которой при оптимальном объеме капитала доход будет максимальным. Для упрощения дальнейшего анализа мы будем полагать, что фактор c является простейшим, т.е. неразложимым на составляющие. Факторы CP и d также являются простейшими, тогда как факторы s и L являются композитными и подлежат дальнейшему уточнению. Формула является первоначальным вариантом факторной модели доходности.

Фактически мы выделяем объективно присущие инвестиционному процессу риски, т.е. такие, которые инвестиционный процесс несет в силу своей природы и механики ценообразования:

1. Ценовой риск – риск неблагоприятного изменения цены.
2. Риск изменения волатильности – риск снижения/повышения волатильности и, как следствие, искажения ценовой информации.
3. Риск ликвидности – риск невозможности совершить необходимую операцию ввиду отсутствия контрагента.

Предположим, что мы располагаем данными демонстрационного тестирования инвестиционной стратегии за период T, которое может проводиться на базе любого программного обеспечения. С учетом построенной факторной модели доходности очевидно, что основным фактором, влияющим на исход сделки, является s-ценовой сдвиг, который может быть как благоприятным (положительным), так и неблагоприятным (отрицательным). Ценовой сдвиг мы можем определить как эффективное расстояние с момента открытия сделки до момента ее закрытия. То есть период, за который рассчитывается сдвиг, находится на временной шкале между моментов открытия и моментом закрытия сделки. Немаловажно в данном случае время открытия сделки, т.к. рыночные цены подвержены флуктуациям и значения цен непрерывно изменяются. В то же время известно, что рыночные цены и образуемые ими формации являются в определенных случаях статистически предсказуемыми, из чего следует вывод, что реализуемый параметр s во многом определяется моментом совершения операции и моментом ее прекращения. То есть действия менеджера, направленные на выбор идеального момента открытия сделки, во многом определяют ее исход. При этом выбранный момент может быть как благоприятным, так и неблагоприятным. В общем случае среднее значение параметра s зависит от:

• Вероятности выбора менеджером благоприятного момента для совершения операции.
• Среднего положительного и среднего отрицательного значений параметра s.

Говоря проще, чтобы реализовать положительный параметр s, инвестиционный менеджер должен совершить сделку в благоприятный момент времени, а сила ценового движения должна быть большой, чтобы реализовать как можно больший его модуль. Отметим важный факт: выбор благоприятного момента времени для совершения операции автоматически не влечет за собой высокой волатильности параметра, т.к. условия для совершения операции определяются постфактум, тогда как величина параметра определяется уже в течение операции. Для того чтобы показать влияние фактора вероятности, мы должны рассмотреть математическое ожидание параметра s[3].

Вероятность выбора менеджером благоприятного момента обозначается параметром p(s) и может быть рассчитана на основе тестовых данных в любой современной программе технического анализа по формуле:

p(s) = Qs/n

Где, Qs - количество сделок с положительным эффективным расстоянием; n - число сделок, n принадлежит N.

Среднее положительное и среднее отрицательное значение параметров определяются по формуле:

E(s > 0) = SUM sn / n

или

E(s < 0) = SUM sn / n

Где, sn - сумма пройденного положительного или отрицательного расстояния за все совершенные операции.

Тогда математическое ожидание E(s) можно также выразить формулой:

E(s) = E(s > 0) x p(s) + E(s < 0) x (1 - p(s))

Возможно также дальнейшее уточнение составляющих параметров величины s, однако для наших целей вполне подходит эта формула. Соответственно, все значения всех переменных для данной модели берутся из временного интервала инвестиционного цикла T.

Суммируя доводы, мы получаем следующую модель оценки величины доходности m серии сделок n периода T и одновременно формулу ее математического ожидания:

Где, d - доля капитала, участвующая в серии сделок; L - моментальная ликвидность.

Отвечая на вопрос, как учитывать риски инвестирования, необходимо для каждого фактора рассчитать доверительный интервал для каждого композитного параметра, используя формулу математического ожидания нормальной выборки. Выбирая наихудшее значение доходности, мы можем учесть риски, связанные с описанными нами факторами, при определении доходности.

Общий алгоритм аллокации финансовых ресурсов

Общий подход к аллокации финансовых ресурсов строится исходя из цели максимизации прибыли экономического субъекта. В связи с этим, определив показатель доходности инвестиционной стратегии, необходимо принять решение относительно целесообразности финансирования ее внедрения и, в случае целесообразности, решение относительно выбора источника финансирования.

Первоначально стоит сравнить получившийся показатель доходности с величиной MAR фонда для фиксированного периода времени.

Minimum Acceptable Return (MAR) – минимальная требуемая доходность, расчетный показатель, задаваемый инвестором исходя из определенных побуждений.

В качестве величины MAR могут быть приняты безрисковая (банковская) ставка доходности или минимальная ставка доходности по имплементируемым инвестиционным стратегиям. После того как была получена такая инвестиционная стратегия, показатель доходности PI превысил MAR (иначе говоря, имеет смысл изъять средства из одной системы с целью перевода в другую), стоит проанализировать устойчивость инвестиционной стратегии к изменениям. Из формулы видно, что причинами снижения эффективности инвестиционной стратегии могут являться:

1. Снижение уровня ликвидности.
2. Рост объема капитала в обороте.

Так как функция доходности является квадратичной, то существует теоретически оптимальный объем капитала, при котором доходность достигнет максимума. Зная уровень доходности инвестиционной стратегии и координаты вершины параболы, мы можем также рассчитать приблизительно, через какое время стратегия достигнет пика эффективности при неизменности других параметров. Именно на основе этих данных и должны приниматься решения касательно аллокации финансовых ресурсов между различными стратегиями и именно в этом направлении необходимо продолжить исследования.

Литература:

1. Бендер Дж., Нильсен Ф. Фундаментальные аспекты фундаментальных факторных моделей // MSCI Research lnsight. Июнь 2010. 15 с.
2. Блау У., Кауфман П.Дж. Моментум, направленность и расхождение. М.: Пер. с англ. М.: ЕВРО, 2003. 171 с.
3. Булашев С.В. Статистика для трейдеров. М.: Компания Спутник+, 2003, 245 с.
4. Бригхэм Ю., Эрхардт М. Финансовый менеджмент. 10-е издание. СПб.: Пер. с англ. СПб.: Питер, 2010. 960 с.
5. Коггин Д.Т., Хантер Дж. Е. Проблемы оценки качества инвестиционной информации // Financial Analysts Journal. Май/Июнь 1983. С. 25-33.
6. Кургузскин А.А. "Биржевой трейдинг: системный подход"
7. Мостеллер Ф., Рурке Р., Томас Дж. Вероятность. М.: Пер. с англ. М.: МИР, 1999. 433 с.
8. Савчук В.П. "Оценка эффективности инвестиционных проектов"
9. Труничкин Н., Яковенко К. "Неуловимые тренды", журнал "Фьючерсы и опционы". Март 2012. С. 76-80.
10. Чернов А. "Методика принятия решения о совершении трейда на основе оценки риска", материалы конференции "Вопросы системной торговли", 03.10.2003.
11. Фабоцци Ф. Дж. Управление инвестициями. М.: Пер. с англ. М.: ИНФРА-М, 2000. XXVIII, 932 с.
12. Шарп У.Ф., Александер Т.Дж., Бэйли Д.В. Инвестиции. Пер. с англ. М.: ИНФРА-М, 2001. XII, 1028 с.

Источник: Парасоцкая Н.Н., Писанов А.В. Факторная модель анализа эффективности инвестиций // Финансовый вестник: финансы, налоги, страхование, бухгалтерский учет. 2012. №10. С. 15-26.